ML08. Unsupervised Learning

1. Clustering

1.1. unsupervised Learning : introduction

• unlabled data로부터 작업하는 unsupervised learning이다. (y값이 없고 x값만 있는 형태이다)
• “find some structure“이 목표이다. -> clustering algorithm
• ex) market segmentation, social Network analysis, Organize computing clusters, astronomical data analysis

1.2. K-Means Algorithm

• automatically clustering algorithm
• 1. randomly initialize the cluster centerorids
• 1. move centroids(move them to the average of the same color, new mean)
• 1. new centriod에 따라 새롭게 group을 형성한다
• 1. 다시 new centroid를 정한다. 이 형태를 반복한다. (until converce)
     
• 위에서 $c^i$는 해당 원소로부터 가장 가까운 centroid인덱스이다. 따라서 각 원소로부터 거리를 최소로 할 수 있는 k에 대해 아래의 식이 성립한다.
• 또한 M의 값은 중심의 값을 계속해서 수정하는 형태로 실제로 분류된 값들 중에서 average값으로 중심을 계속 이동하는 것을 의미한다.

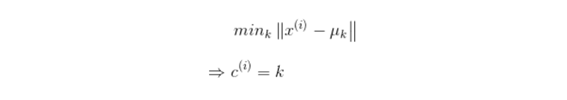
• k-means for non-separated clusters인 경우에도 마찬가지로 k값만 정한다면 clustering은 가능하다 ex) height와 weight에 따라 T-shirts size를 정하는 경우 k=3(non-seperated의 형태여도 상관없음)

1.3. optimization objectives

• 비용함수를 최소화하는 형태로 최적화하는 형태는 항상 존재한다(여기서도 마찬가지)
• 비용함수는 각 data x의 값과 x가 속하는 cluster의 중심값과의 거리가 최소화되는 형태의 cost function으로 나타낼 수가 있다.
• 이 비용함수를 최소화하는 cluster centroid를 정하며, 각 중심점을 정하는 것이 최적화하는 방법이다.

• 결국 kmeans를 설명하는 for loop알고리즘을 보면
  1. clustering assignment step에서는 Mu를 고정하고 $c^(i)$에 대해서 J를 최소화 한다.
  2. move centroid step에서는 $c^(i)$를 고정하고 mu에 대해 J를 최소화하는 방법이다.
• 즉 위의 두 식을 종합하면 결국은 kmeans 알고리즘 자체가 비용함수를 고려한 optimiazation objective를 만족한 형태라는 것을 알 수가 있다.

1.3. Random initialization

• random initiatization은 결국 kmeans가 local optimum에 도달하는 문제점을 해결할 수도 있다.
• ”Randomly initialize K cluster centroids M1,…, Mk“의 정확한 의미는?(=애초에 cluster의 중심좌표를 잡는 방법은?)

• 실제로 initializer가 잘못된다면 stock to local optimum이 될 수가 있다.

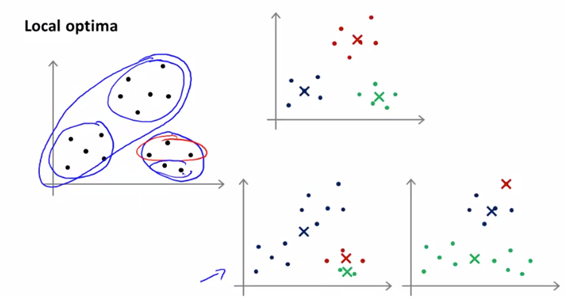
• 따라서 local optimum을 피하기 위해, 좋은 clustering(optimization고려)를 얻기 위해 random initializer를 이용하여 k-means를 여러번 돌려볼 수가 있다.
• 100번을 loop를 통해 100번의 clustering결과를 나올 수가 있다. 각각에 대해 cost를 계산하고 최소의 cost를 가지는 값을 계산한다.

1.4. Choosing the number of clusters(=how to get K)

• k값을 선택하기 위한 방법으로 elbow method를 사용한다 : k값의 변화량에 따라 distortion function J값이 급격히 감소하는 지점을 선택하는 방법이다.
• 하지만 elbow method가 애매할 경우에는? (아래의 오른쪽 그림과 같은 경우 )

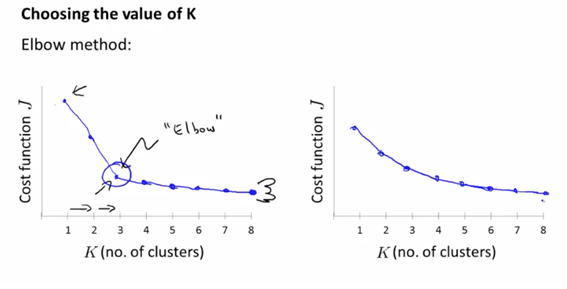
• elbow method가 애매한 결과로 작동할 경우에는 단순히 클러스터링으로 얻는 것도 중요하지만 어떤 k를 사용해야 수지타산이 맞을지를 비즈니스 적인 관점에서 판단해야 한다.
• 혹은 실루엣 분석을 사용할 수도 있다.

2. Dimensionality Reduction(=차원축소)

• unsupervised learning중의 다른 기법인 Dimensionality Reduction을 공부한다
• 차원축소의 목적 :
  1. data compression
  2. data visaulization

2.1. motivation : Data compression

• 꼭 중복된 feature에 대해서만 차원을 축소할 수 있는 것은 아니다.
• 차원을 축소하면 일부 정보가 유실된다, 어떤 경우는 데이터의 차원을 축소하면 잡음이나 불필요한 세부사항을 걸러낼 수가있다(=아래의 2D 그래프는 highly redundant data 이다)
• 데이터의 한 축을 pilot skill, 다른 한 축을 pilot enjoyment라 하고 두 feature간 관계를 거의 직선으로 나타낼 수 있다고 하다. 이 새로운 직선을 pilot aptitude라 부르고 두 개의 feature을 대신하는 새로운 feature로 z를 사용할 수가 있다.
• prejection(투영)방법을 사용하면 ”새로운 공간에 투영”하는 형태이므로 새로운 feature - vector가 생성된다고 이해한다. (다른 방법으로는 manifold방법이 있다->뒤틀린 데이터의 경우 사용한다)

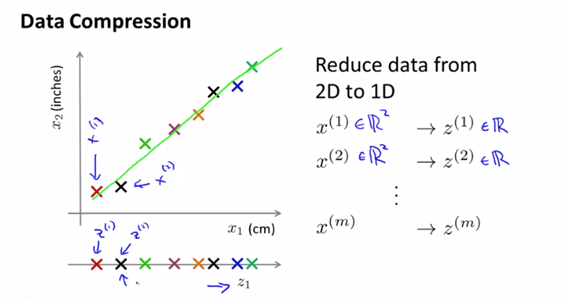
• 위와 같은 그래프를 참고하면 highly redundant data이기 때문에 하나의 dimm으로 줄이는 것이 가능하다.(굳이 2개의 축을 두고 있을 필요가 없다는 의미, 필요없는 데이터는 알아서 삭제되는 형태의 차원축소) 이에 따라 새로운 feature인 z1의 정의가 가능하고 data compression이 가능하다.

• data compressin 3D->2D
• 3D데이터를 2D로 만들기 위해 투영의 방법을 사용하여 하나의 초평면 위에 나타냈고 이 초평면의 위치를 나타내기 위해 z1, z2라는 새로운 feature을 생성했다. 이에 대해 2D형태의 데이터가 생성되었다.

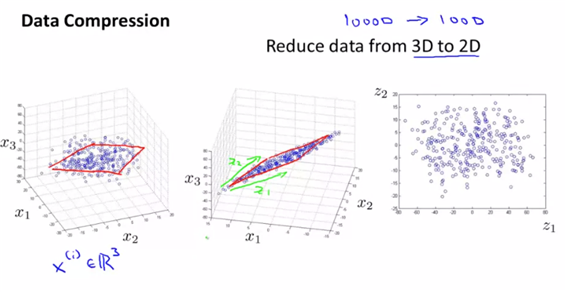
2.2. motivation 2: data visualization

• 효과적인 모델을 작성하기 전에 많은 feature가 있을 때 feature을 줄여서 데이터에 대한 intuition을 얻을 수가 있다.

• 500개의 feature을 2개로 줄여 그래프로 나타내면 아래와 같다(어떤 성분값에 따라 country가 영향을 받는지를 직관적으로 알 수가 있다)

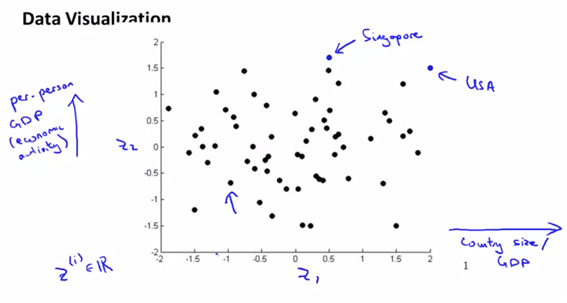
• Q)　각 feature의 z1, z2가 뭘 의미하는지 실제로 알수는 있는가? :
• 실제 python으로 분석시 알 수는 없다.

3. Principle Component Analysis

3.1. principle components analysis problem formulation

• lower dimention인 평면을 찾는다. 실제 data와 line사이에 lower distance인 값을 찾는다.(=projectoin error를 최소로 하는 선을 찾는다, 반면에 자주색 선은 최대의 projection error값을 가진다)

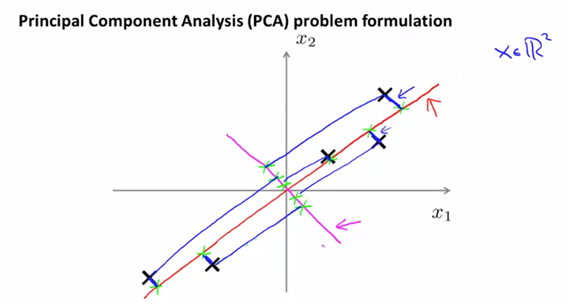
• n차원을 k차원으로 축소할 때는 각 데이터를 k개의 벡터 u에 대해 투영시켰을 때의 projection error를 최소로 하는 벡터 u를 찾으면 된다. (즉 k개의 direction을 찾으면 된다)

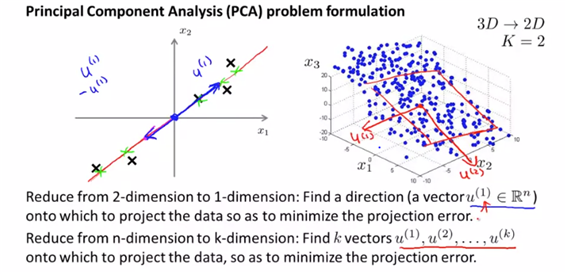
• 다음 주성분을 찾는 방법 : projection error를 최소화하는 축을 선정하고, 그 축과 직교하면서 projection error을 최소로 하는 축을 선정하는 형식으로 선정할 차원의 수만큼을 반복한다.
• and PCA is not linear regression : 고려하는 “거리”가 다르다, PCA는 predict할 y가 존재하지 않는다.

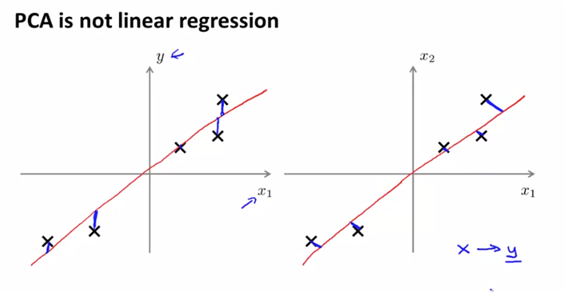
3.2. principle component analysis(=PCA) algorithm

• pca전에는 preprocessing step을 거친다. 이는 feature간 스케일이 다르기 때문에 비교할 만한 스케일을 얻기 위함이다.

• sum of the projection error을 최소화하는 u(1)을 구한다. (만약 2차원이라면 u(1)과 이에 직교하는 u(2)를 구한다)
• PCA를 선택하는 방법 :
• 벡터상의 covariance matrix를 계산한다.

• PCA의 목적은 원데이터의 분산을 최대한 보존하는 축을 찾아 투영하는 것이다. 평균 0으로 조정(=전처리의 결과)한 데이터셋 X를 단위벡터 e인 임의의 축 p에 투영한다고 했을 때 X의 투영된 결과는 Xe라고 표현할 수 있다. 위는 데이터 x를 축벡터 e에 대해 투영한 데이터의 분산을 계산한 값이다.

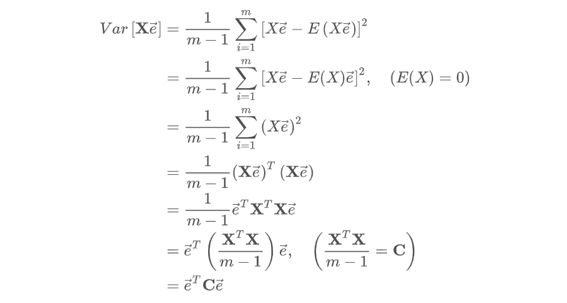
• 결국 목적은 아래와 같고, 아래의 목적을 달성하기 위해 SVM에서 사용했던 것과 같이 라그랑제 승수법을 사용하여 아래의 식을 최대화할 수 있는 c값을 찾는다.

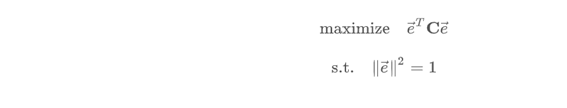
• 결국 위의 식에서 e는 C의 고유벡터이며 $\lambda$는 C의 고윳값이다(특잇값분해에 의하면). 여기서 고유벡터의 열벡터를 주성분이라고 한다. 즉 고유벡터에 투영하는 것이 분산의 최대가 된다. (고유벡터가 주성분이므로)

• n dim-> k dim일 때 위의 U 벡터에서 k개의 칼럼을 선정하여 주성분으로 사용한다.

PCA details

• 참고 :　https://1ambda.github.io/data-analysis/machine-learning-week-8/

  4. Applying PCA

  4.1. Reconstruction from compressed representation

  4.2. choosing the number of principle components(k)

• 데이터 전반으로 봤을 때 “projection error”를 최소화 하면서 “각각의 데이터에 대해서는 total variation”을 가장 크게 투영할 수 있는 값의 k를 골라야 한다.

• 아래와 같이 k값을 조정해가면서 check과정을 거친다. 마지만 체크포인트를 만족하지 못한다면 다시 k값을 조정하여 계산하는 방법을 가진다.
• 혹은 SVD를 적용하면 S의 대각선에 있는 값들은 값이 큰 순서대로 나열되어 있는 형태이므로 k값이 선정됨에 따라 확률적으로 계산하여 선정할 수도 있다. ( 만약 값이 크다면 k가 작은 값이어도 많은 값을 가질 수 있다는 의미이므로, k값을 작게 가지는 것이 가능)

4.3. Advice for applying PCA

• 차원축소를 사용하는 가장 대표적인 이유가 supervised learning의 speed up이다.
• 만약 가지고 있는 데이터가 100 feature을 가지고 있다고 하면 SVM을 돌리던 다른 모델을 돌리던 간에 성능이 낮아진다. 이런 경우에 어떻게 PCA를 사용하는지에 대해 설명하고자 한다.
• 주의할 점은 U를 찾을 때 training set에만 하고 cross validation이나 test까지 포함해서 U를 찾으면 안된다. 나중에 training set으로만 찾아낸 U를 이용하여 CV, test에 대해서 다시 PCA해야 한다.
• PCA의 응용 :
  • reduce memory, disk needed to store data
  • speed up learning algorithm
  • visualization
• PCA를 사용하면 feature의 수가 줄기 때문에 overfitting을 방지하기 위해 사용할 수도 있다고 생각할 수 있지만 사실은 regularization을 사용하는 편이 낫다. 왜냐하면 PCA는 y값이 없는 상태에서 작동하므로 y를 고려하지 않은 데이터가 손실이 발생할 수 있다. 다만 1%가 손실된다고 하더라고 y와 관련하여 아주 중요한 정보일 수도 있다.
• 무작정 PCA부터 적용하는 경우도 마찬가지로 잘못된 경우이다. original x에 대해 알고리즘을 구현해보고 결과가 별로일 때 PCA를 구현한다.

Reference

• https://1ambda.github.io/data-analysis/machine-learning-week-8/
• machine learning by Andrew NG