ML07. Support Vector Machines

1. Large margin Classification

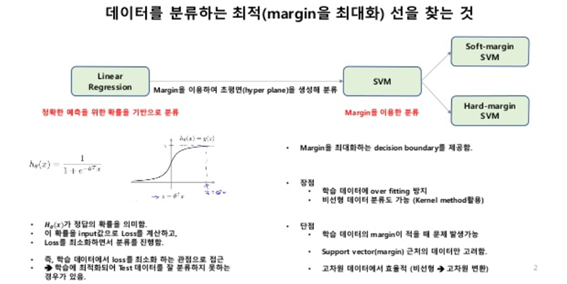
• SVM은 기본적으로 데이터를 분류하는 최적(margin을 최대화)하는 초평면을 찾는 것
• regression은 정확한 예측을 위한 확률을 기반으로 분류하며 loss를 최소한으로 하고자 하는 것이 목표였다면 SVM은 margin을 최대화 하는 decision boundary를 제공하고자 하는 것이다.
• decision boundary : 가중치 벡터(=$\theta$, W)에 직교하면서 margin이 최대가 되는 초평면을 찾는 것이 최적
• margin이 커지면 학습 데이터에 최적화되지 않고 실제 데이터의 분류 정확도가 향상된다고 본다.
• 그렇다면 모델을 최적화하는 방법은?(=decison boundary구하는 방법?)

1.1 optimization objective

• SVM에 대한 직관적인 이해를 위해 logistic regresssion과 비교하여 cost function작성한다.

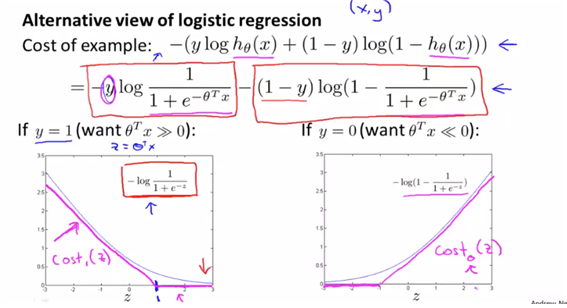
• logistic의 cost function은 앞에서 배운 것과 같이 위와 같고, 그를 그림으로 그린 바이다. y=1, y=0일 때를 나눠서 각각 그래프로 그린 값이고 이를 단순화하여 z=1을 기준으로 변형하여 그래프를 그린 형태가 $cost(z)_1$과 $cost(z)_0$이다.
• 결국 SVM의 cost function은 logistic에서 약간 변형한 형태이다.
• logistic의 식을 단순한 값으로 치환하여 나타내면 아래와 같다 (아래에서 lambda는 결국 low cost의 값과 small parameter을 유지하게 하는 regularization값이라고 생각한다.

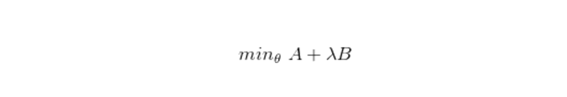
• 위의 식에서 $\lambda$는 regularization term으로서 small parameter B를 조절하는 역할을 한다. 따라서 위의 식을 변형하여 다시 써보면 min(CA+B)의 형태이다.

• 왜 이렇게 변형할까?? -> C값이 커진다면 A=0이 된다(=오분류가 거의 없도록 한다) 이에 따라 B의 term만 고려하면 되므로 식을 더 간단하게 이해하여 minimize하기가 쉽기 때문이다(=theta값만 최소화하면 된다)

• C는 $1/\lambda$로 작은 람다를 사용하면 B가 커지고 C도 커져 A를 낮추고 B를 높이는 것과 같다. 즉 C를 쓰느냐 $\lambda$를 쓰느냐는 어떤 항을 옵티마이제이션의 중심으로 두느냐의 차이이고 최적화된 파라미터를 찾는 것은 같다고 본다.
• 다음은 최종적으로 정리한 cost 식이다. 다시 한마디로 정리하자면 결국 regularization term을 두는 원리는 같되, 어떤 parameter을 기준으로 두어 정리하는지의 차이이고, 어떻게 조절하고자 하는지의 차이라고 본다.

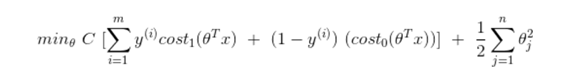
1.2. Large margin intuition

• 사람들이 SVM을 Large Margin Classifier이라고 부른다.
• 아래의 SVM의 cost function에 따르면 이를 minimizing하기 위해서는 몇가지의 조건이 필요하다.
• 그렇다면 저 cost0, cost1식은 어디서 왔을까? 기본적으로 w.T*x식이 decision boundary식이고 margin을 둔 식이 아래의 두 식이라고 생각하면 된다.

• 만약 C가 매우 크다면 그 항에 곱해지는 term은 0에 가까운 값일 것이다.

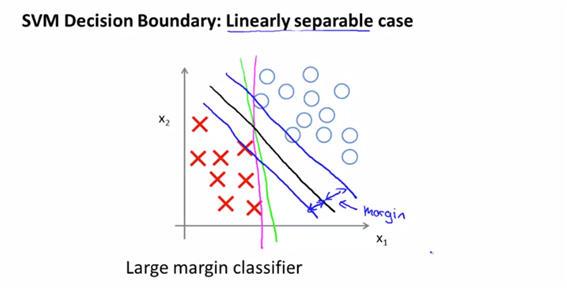
• SVM이 decision boundary를 가지는 형태를 보면, margin을 가지는 것을 볼 수가 있다.
• 그 decision boundary를 구하는 가장 좋은 방법은 large margin을 가지는 값을 구하는 거 것이다.

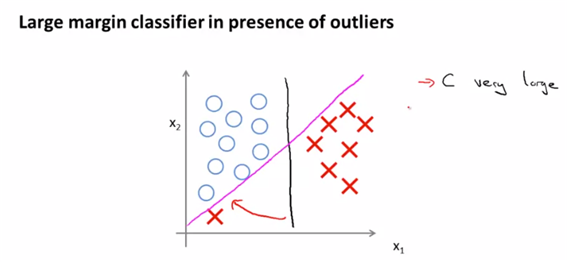
• C의 값이 매우 커진다면(=regularization term에 영향) outlier에 매우 민감해질 가능성이 높다. 왜? C의 값이 커진다는 것은 regularization term의 값이 작아진다는 말고(lambda의 역수가 커지므로 lambda는 작아진다는 말과 동일하므로) 같고 그것은 결국 overfitting될 위험이 크다는 것을 의미한3다. 따라서 outlier값에 민감해 지므로 좋은 형태는 아니다.(자주색 선)
• 그러나 C가 그렇게 큰 값이 아니라면 비정상적인 샘플은 적당히 무시하고 검은색 선을 찾아낼 수 있게 된다. 이것이 SVM이 작동하는 방식이다.

• 즉 large margin을 찾기 위해 cost 식을 CA+B의 형태로 변형했고, theta값을 작게 만드는 형태로 변형했다.

1.3. Mathmatics behind Large Margin Classification

• 내적을 계산하는 원리 : (투영이라는 것은 해당 벡터에서 직교점을 내렸을 때의 점을 의미한다) U.TV=pu의 형태로 정의할 수가 있다. 두 벡터사이의 각이 90도를 넘어가면 –값으로 넘어간다고 보고 식은 동일하다.(여기서의 p는 projection의 투영된 길이값이다)

• large margin classifier에 있어서 어떻게 optimization이 이루어지는지를 알 수있게 하려고 한다.
• cost function식에서 C값이 매우 크다고 하면 결국 남는 cost 식은 아래와 같고 이를 min하려고자 한다.
• 식을 더 직관적으로 보기 위해 n=2, $\theta_0=0$으로 정의하고 계산한다.
• theta transpose * x의 값을 알아야 최종적으로 classifiaction을 결정할 수가 있으므로 그 내적을 구하기 위해 그래프를 그리면 아래와 같다. 또 내적의 정의에 의해 theta의 길이와 projection을 곱한 값을 이용하여 값을 구한다.

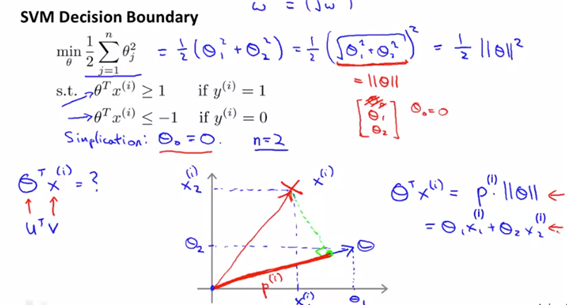
• 결국 위의 min(J(theta))를 만족하게 하는 theta값을 찾으려고 하는 것이 최종적인 optimiaztion objective이고, decision boudary에 해당하는 h(x)=theta.T*x이므로 이 h(x)의 범위에 따라 classifiaction이 달라진다고 할 수 있다.

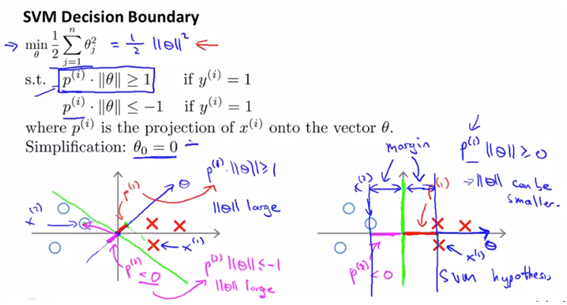
• 위의 그림을 생각했을 때, 왼쪽의 형태는 애초에 large margin이 아니므로 best한 optimization objective를 만족하지 않았다고 볼 수가 있다. 또한 이 형태는 cost function을 minimize하는 값이 아니므로 optimized된 값이 아니다. 투영된 길이의 p의 값이 매우 작으므로 벡터 theta의 norm이 커야 하기 때문이다.
• 반면 오른쪽의 그림은 투영된 길이의 p가 크므로 theta값이 작으므로 원래 작게하고자 하는 cost값이 작아지므로, 우리가 원하는 형태를 만들어 볼 수가 있다.

2. Kernels

• 선형분류가 어려운 저차원의 데이터를 고차원의 공간으로 매핑하는 함수이다.
• 고차원의 공간으로 매핑하는데 있어(=feature의 수를 늘린다는 것) kernel함수의 종류는 여러 가지 인데 여기서는 가우시안 커널법을 주로 사용한다.

  2.1. kernels1

• 여기서는 SVM을 complex nonlinear classifier에 적용해보고자 하고 그 방법을 “kernel”이라고 한다.

• non-linear 형태의 데이터에 대한 decision boundary를 적용하려면 위와 같은 형태의 식이 필요하다. 이를 f식으로 대체한다고 하면 뭐가 더 나아질까? (실제로 고차다항식은 계산비용이 너무 비싸다..)
• 즉 위와 같이 새로운 feature의 f로 대체하여 사용하기 위해 새로운 feature을 생성해보도록 하겠다.

• 수동으로 몇 개의 landmark를 고른 후에 이 landmark와의 거리로 새로운 feature의 f를 만들어보고자 한다. 여기서는 similarity를 기준으로 만들었으며, 이는 Gaussian kernel이라고 부른다.(어떤 커널식을 사용하느냐는 최적화의 문제이다. 다항식을 대체하기 위한 새로운 feature값의 형성 )

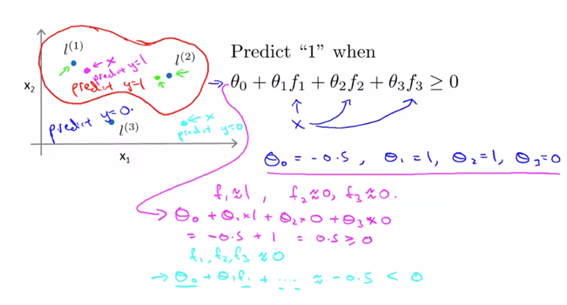
• 결국 x와 l1이 가까운 값이면 feature f1은 1이 되고, x와 l1이 먼 값이면 feature f2는 0의 값이 될 것이다.
• 즉 landmark와의 “거리”를 기반으로 feature f를 생성하며 h(x)를 기반으로 classification을 진행하는 것을 의미한다. –> non-linear 형태의 복잡한 형태의 classification을 SVM방법을 사용하여 분류하는 방법을 의미한다

2.2. Kernel 2

• 그렇다면 landmark는 어떻게 정하는가?
• 1. 학습 데이터를 읽어온다(given x)
• 1. 학습 데이터별로 landmark를 생성한다(=학습데이터와 동일한 위치)
• 1. 새로운 샘플이 주어지면 모든 landmark와의 거리(f)를 계산한다

• 그렇다면 결정된 f값을 SVM에서 어떻게 활용하느냐?

SVM parameters

• 1. parameter C(=1/lambda)

• 1. parameter sigma square

• 즉 C의 값이 크거나 sigma의 값이 작다면 overfitting의 위험에 처할 수 있다.

• 그렇다면 “커널 트릭”의 의미는?
• 매우 고차원으로 변환한다면 고차원 데이터를 SVM으로 연산하는 것은 너무 많은 연산비용이 소모되어 사용이 어렵다. 이에 따라 사용하는 것이 Kernel Trick이다. 수학적으로 고차원의 데이터인 a,b를 내적하는 것과 내적한 결괄르 고차원으로 보내는 것은 동일하다. (직접 내적하는 것이 아니라 내적한 결과를 보내는 것). 이를 활용하면 모든 계산은 원 데이터 차원에서 이루어지게 된다.

3. Using an SVM : 커널선택

• 1. kernel을 선택하지 않으면 -> linear kernel
     • 기본 linear classifier으로 동작한다.
     • 어떤 경우에 사용할까?
     • feature n이 크고
     • training data m이 작고
     • 고차원 feature인 경우 overfitting의 위험
• 1. Gaussian Kernel
     • sigma값을 정해야 한다, kernel함수의 정의
     • feature이 작고 training data 가 큰 경우 -3. 다른 커널들
     • polynomial kernel : 음수를 가지는 데이터가 없는 경우에 사용
     • String Kernel, Chi-square Kernel : 소수의 문제해결에 사용

reference

• 강의 내용 정리한 ppt(매우 잘 정리되어 있음. 전체적인 맥락+수식 파악하기에 용이함) : https://www.slideshare.net/freepsw/svm-77055058
• 강의 참고 : coursera Andrew Ng professor‘s machine learning class