ML06. Practical advices

1. Evaluating a learning algorithm

앞에서는 regression에서의 gradient descent방법, 신경망에서의 backpropagation에 대한 방법을 축으로 설명을 했었다. 하지만 기본 이론의 경우와 머신러닝을 실전에서 사용하는 방법은 다르다. 따라서 이를 활용할 수 있는 팁들을 설명한다. 또 마지막에서는 스팸분류기를 통해 간단한 머신러닝 시스템을 설계해 볼 수가 있다,

(1) deciding what to try next

• improve algorithms(we have done trouble for errors in our predictions)
• when we predict housing prices, when the test of my hypothesis on a new set of houses, what can I do then?
• get more training examples
• try smaleer sets of features
• try getting additional features
• try decreasing or increasing $\lambda$
• machine learning diagnostic : know what is working or not and how to improve the performace of the system.

(2) Evaluating a Hypothesis

• 단순히 low error을 갖는다고 좋은 것은 아니다. 과적합의 위험이 있기 때문이다.
• linear regression

• logistic regression

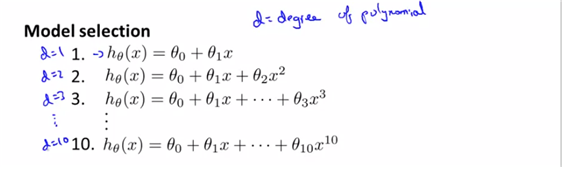
• (각 식에서의 theta값은 min cost function에 해당하는 값이다.) 그에 대해 vectorized theta값을 정의한다. 어떤 d를 선택해야 최적의 값일까?
• 각각에서 나오는 파라미터 벡터에 대해 테스트셋 에러인 J함수에 대해 이 비용함수를 최소로 나오게 할 수 있는 d를 가진 모델을 선택한다.
• 하지만 마찬가지로 test, trainset에만 optimistic estimate of generalization error가 있을 수 있다. 즉 실제 데이터 상에서는 똑같이 적은 에러를 보여줄 것이라 확신하지 못하기 때문이다.

Train/validation/test error

• 위에서의 optimistic estimate of generlization error를 해결하기 위하여 trainset을 60%/20%/20%로 나누어 각각 training set, cross validation set, test set이라 하기로 한다. 그리고 각각에 대해 에러를 구할 수 있다.

• 즉 theta를 trainset에 학습하여 J를 최소화하는 theta를 얻은 후에 cross validation set에 대해 error을 구해 가장 작은 값을 갖는 모델을 고른다.(최적의 d값을 가지는 경우를 구할 수가 있다. )

• 선정한 model에 대해 test error을 구하면 이는 테스트셋에 대해 fit하지도 않고, 가장 적은 에러를 가지는지 검사되지도 않은 데이터이므로 일반적인 에러값에 대한 추정치라고 할 수가 있다

2. Bias vs Variance

**(1) Diagnosing Bias vs Variance **

• cross validation error : cross validation은 주어진 데이터를 일부 나누어 한쪽 데이터로는 학습시켜 모델을 만들고 나머지 학습시키지 않은 데이터로 그 모델에 대해 검증하는 방법이다. 즉 70%의 모델을 만든 형태와 나머지 30%검증하는 형태의 차이를 가지고 cross validation error이라고 한다.
• 아래 그림에서 확인 가능하듯이 training eror을 그려보면 degree of polinomial이 낮을수록 error는 높을 수밖에 없다. 왜냐하면 data에 더 fit되는 형태를 그리기가 힘들기 때문이다. 반면에 CV set에 대해서는 하나의 d만 최저치를 가지고 나머지는 그보다 높기 때문에 아래와 같은 그래프를 그릴수가 있다.
• (왜? cross validation은 하나의 dataset내에서도 70%와 30%로 나누어 에러를 측정하므로 너무 overfit된 경우도 에러로 인식하기 때문이다)

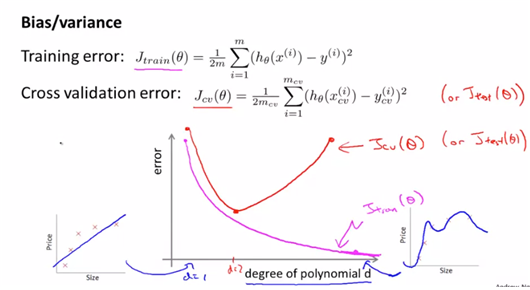
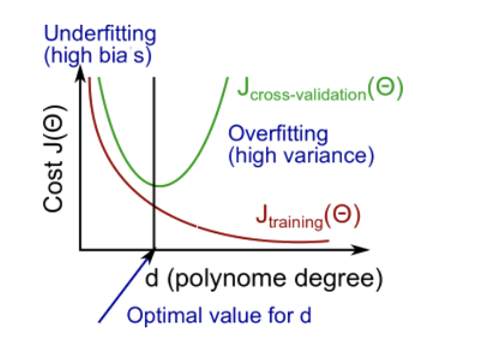
• CVset과 test set에 대하여 degree가 달라짐에 따라 error값이 달라지고, 이에 따라 high bias, high variance가 달라진다고 할 수가 있다.

(2) Regularization and Bias/Variace

• 보통의 비용함수에 regularization term을 씌우고 lambda값에 따라 overfit되는지 underfit되는지가 달라진다.
• lambda가 크면 high bias이고 매우 작으면 high variance의 상태가 된다. 적당한 중간값을 고를 수 있는 방법은 무엇일까?

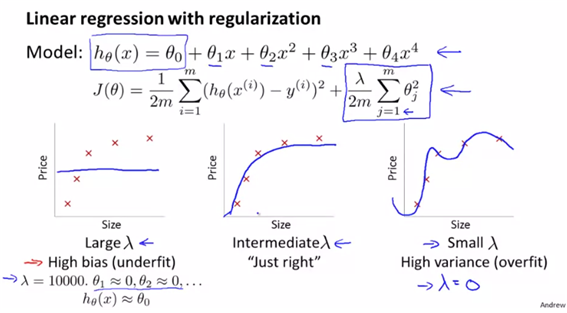
• 그렇다면 lambda값은 어떻게 정할까?

• model selection에서의 방법과 유사하다. lambda를 점진적으로 증가시키면서 각각의 J(theta)를 최소화하는 theta값을 잦는다. 그리고 theta를 이용하여 $J_cv(\theta)$가 최소화되는 lambda를 구한다.
• 앞에서 말했듯이 lambda가 작으면 high variance문제가 발생하고, lambda가 크면 high bias문제가 발생한다.

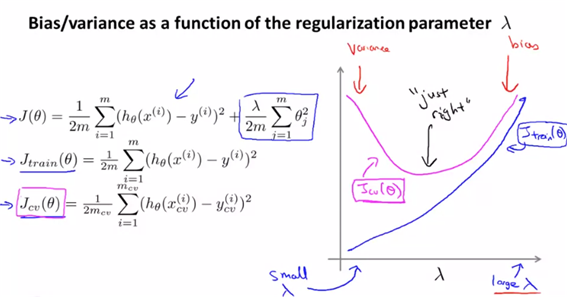
• 이에 대해 error그래프를 그리면 위와 같고, best값은 $J_cv(\theta)$값이 최소가 되는 lambda가 최선의 값이다. (3) learning curve
  
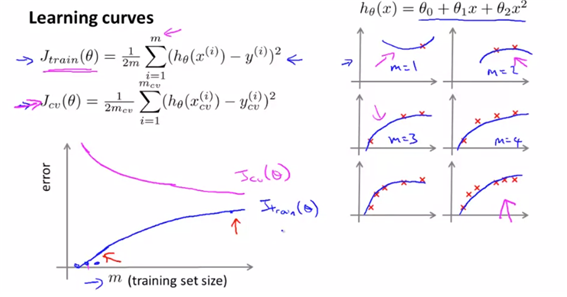
• mean of train error와 mean of cross validation set과 m의 값에 대해 그래프를 그려보면 아래와 같다. 단순히 생각해보면, trainset에 대해서는 size가 작으면 더 잘 fit할 수 있으므로 size가 늘어남에 따라 error값도 늘어나는 것이고, cv는 size가 커질수록 일반화의 가능성이 커지므로 error값이 작아지는 형태이다.
• 아래의 형태가 학습곡선의 형태이다. (기본 idea)

• high bias의 경우에 대해

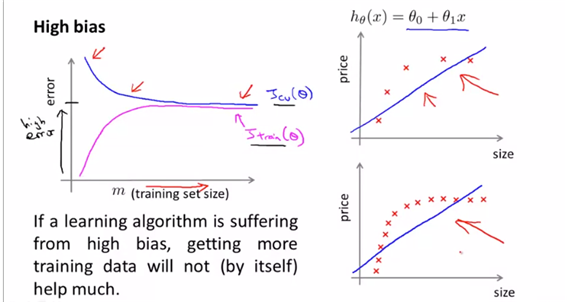
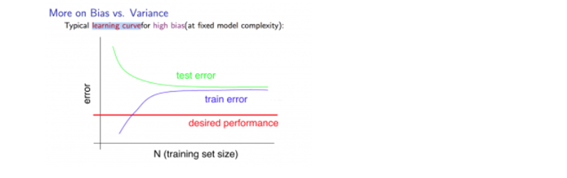
• high bias이면 애초에 형성되는 (수렴되는 ) error의 수준이 높다고 본다.
• cv set에 대해서는 error가 trainset이 늘어남에 따라 줄어들지만, 어느정도의 error를 극복해내지 못하는 형태이고(적절한 일반화가 되지 못하므로), train set에 대해서는 error가 늘어나되, 높은 값으로 높아지는 형태를 띄게 되는 것이다.

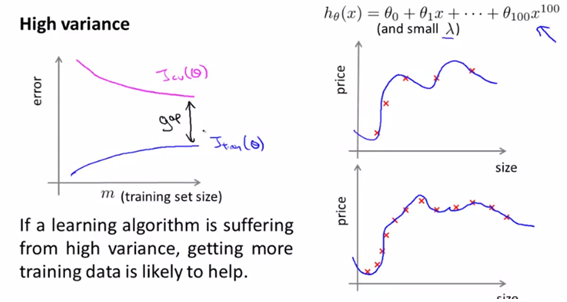
• 이런 경우엔 trainset을 더 많이 모은다고 해서 나아질 문제는 아니다. (일반화의 문제가 아니므로)

• high variance의 경우, polynomial의 degree값이 큰 값이다. (variance가 크려면 dataset에 더 잘 적합했다는 의미가 되므로)

• 이런 경우는 일반화에 있어서의 문제이므로, trainset을 더 모으면 해결될 문제이다.

(4) deciding what to do next revisited

• 처음에 나왔던 6가지의 learning model을 debugging하는 방법은 결국 앞에서 배웠던 경우의 수 (bias, variance)에 따라 달라진다.
• get more training examples -> fixing high variacne
• try smaller sets of features -> fixing high variance
• try getting additional features -> fixing high bias
• try adding polynomial features -> fixing high bias
• try decreasing lambda -> fixing high bias
• try increasing lambda -> fixing high variance

• diagnosing neural network

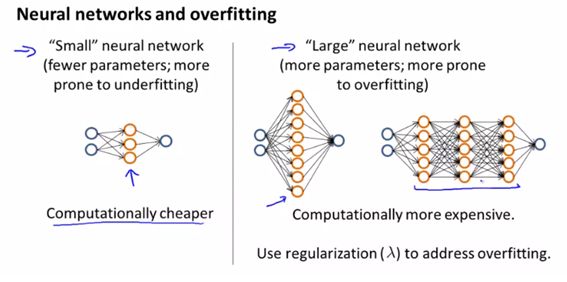
• neural network에 적용하면, ‘small“ neural network를 적용하면 계산이 쉬워지고 underfitting될 위험이 크다. 반면에 ”Large“ neural network를 적용하면 overfitting 될 위험이 크지만 lambda를 이용한 regularization으로 과적합을 어느정도 보완할 수 있다.
• using a single hidden layer is a good starting default. you can train your neural network on a number of hidden layers using your cross validation set. you can then select the one that performs well.

2. building a spam classifier

(1) priortizing what to work on

• supervise learning(classifiaction)
• x=features of email, choose 100 words indicative of spam or not
• y=spam or not
• feature of vector가 그렇게 되면 100개의 차원이 형성이 된다.

• how to spend your time to make it have low error -> collect lots of data or develop sophisticate features based on email routing information(from email header), develop sophisticated algorithm to detect misspellings.

**(2) error analysis **

• recommended approach to machine learning
• 1. start with a simple algorithm that you can implement quickly. implement it and test it on your cross-validation data.
• 1. plot learning curves to decide if more data, more features etc
• 1. error analysis : manually examine the examples that your algorithm made errors on. see if you spot any systematic trend in what type of examples it is making errors on.
     
• error analysis를 하는 방법은 cv error을 발견하면 각각의 에러를 수동으로 검사하여 분류하는 것이다. (cv에러로 분류하여 작업한다 )
• 이메일의 타입이 무엇인지 어떤 feature가 알고리즘에서 이 이메일을 분류하는데 도움이 될지에 대해 생각해 보아야 한다
  
• error analysis는 에러가 나타난 이유에 대한 어떤 경향을 제공할 수 있기 때문에 간단히 먼저 보고 분석해보는 것도 좋다. error analysis는 실제로 분석 결과를 새로운 알고리즘에 적용했을 때 performance가 좋을 지를 알려주지 않는다. 따라서 해보고 numerical evaluation을 비교해 본다.

3. hadling skewed data

error metrics for skewed classes

• cancer classification을 다룬다고 예를 들어보자. only 0.05% of patients have cancer이라고 할 때, skewed data라고 한다.
• 이렇게 확률이 낮은 skewed data의 경우 error을 낮춘다고 해서 좋은 알고리즘이라고 판단하기 힘들어, 에러값말고 다르게 평가하는 방법이 필요하다.
• 이런 경우에 정확도를 측정하는 방법이 precision/recall방법이다.

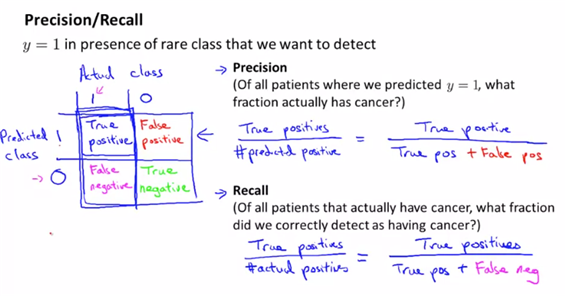
(2) trading off precision and recall

• threshold를 조정하여 기존의 0.5 threshold를 조정할 수가 있다.
• 만약 0.7로 했을 경우는 좀더 확실한 환자만 암으로 진단하기 때문에 precistion은 올라가는 반면 recall은 내려간다.
• 반면에 0.3으로 했을 경우에 덜 확실해도 암이 되는 경우이므로 recall은 높아지지만 예측한 것 중 실제 환자를 의미하는 precisition은 내려간다.
• (more generally : predict 1 if h(x)>=threshold)
• 아래의 그림을 보면 precision과 recall이 tradeoff의 관계라고 볼 수가 있다.

• precision/recall방법은 ‘how to compare precision/recall’을 생각해야 한다.
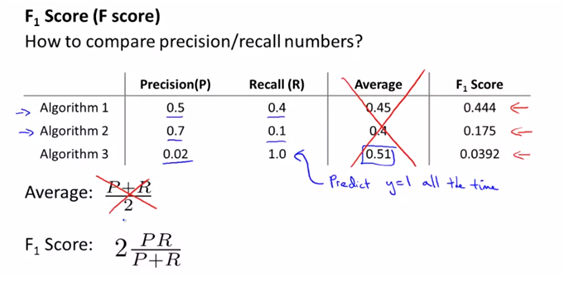
• precison/recall방법 이외에 다르게 평가지표는 F1 score이다.
• 단순히 평균을 하면 극단적인 값이 더 좋은 algorithm으로 나오므로 단순히 평균을 하기 보다는 F1 score을 사용한다
• 따라서 CV set에 대해 높은 F1 score을 가지는 threshold를 택하여 좋은 알고리즘을 사용한다.

5. using large data sets

data for machine learning

• how much data that we have to train
• ex. designing a high accuracy learning system, and algorithm is perceptron(logistic regression), winnow, memory-based, naive bayes
• 위의 4개의 알고리즘을 trainset의 개수에 따라 accuracy를 그려보면 아래와 같다. (data의 수가 많아지면 성능이 더 좋아진다는 이야기)

• 하지만 항상 그렇지는 않다.(항상 데이터가 많다고 더잘 예측하는 것은 아니긴 하다)
• 집값을 예측하는 경우에 feature가 size(.feet)밖에 없는 경우에 y를 예측하는 방법은 무엇일까를 예측하는 것은 어렵다. 즉 정보의 양이 문제가 아니라, 예측하는데 충분한 정보를 전달하는 것이 중요하다는 점이다.
• 정리하자면 충분한 양의 정보를 가지며(=large parameters and have large hidden units), 많은 양의 trainset을 가지면 된다. (과적합의 예방)

reference

Machine learning my Andrew Ng, Coursera