ML03.Logistic Regression
이전에 regression의 optimized theta값을 알기 위해 gradient descent값을 도입했었다. 이번시간엔 classification과 regulrization에 대해 알아보고자 한다.
1. classifiaction
y E {0,1} 으로 나눠지는 것을 classifiction의 가장 기본이다. 이와 같이 calssification에서는 discrete value를 다룬다. multiclass classification도 가능하다.
아래와 같은 경우는 regression으로 문제를 풀면 당장은 맞아보일 수 있으나, 다른 point의 sample이 들어왔을 때, 모양이 크게 변함으로써 정확하게 예측이 힘들 뿐 아니라, 0과 1사이에 regression이 위치하지 않으므로 이해하기가 힘든 단점이 있다.
-linear regression에 threshold를 주는 방식으로 classification을 주는 방식 : 잘 안씀.
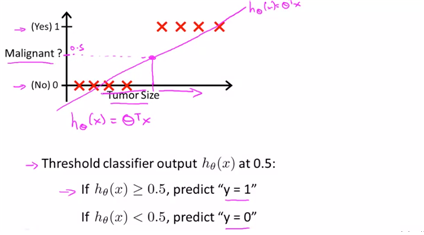
기본적으로 앞에서 배웠던 linear의 형태로 malignant의 prob를 나타낼 수가 있다. 이에 대해 0.5를 threshold로 하여 classification을 적용해 볼 수가 있다.
-만약 additional point가 있다고 한다면, 새로운 linear reg.가 그려질 것이고, 이에 대해 새로운 threshold에 대한 값이 나올 것이고, size에 대한 결과도 다르게 나올 것이다.
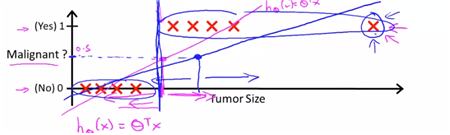
하지만 이 형태는 좋은 형태는 아님. -> 왜? 새로운 point가 정보를 가지고 있지 않기 때문(이상치). 따라서 잘 쓰지 않는다.
또한 classifiation은 0과 1사이의 범위여야 하는데 linear은 그렇지 않다. 이에 따라 classification에서는 regression을 잘 사용하지 않으나, 나오는 것이 logistic regression(logit함수를 적용한 함수라고 이해.) 0~1사이에 regression를 위함.
-hypothesis representation
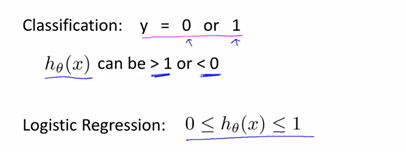
classifiaction을 만드는데 작용하는 hypothesis를 식으로 나타낸 것을 의미한다.
linear로 나타내게 된다면 1보다 큰값이 있거나 0보다 작은 값이 존재할 수 있다.
다음은 h(x)를 0과 1사이의 값으로 나타내기 위해 logit function을 적용한 형태이다.
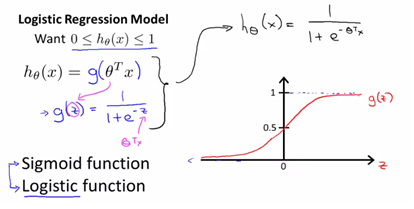
fit the parameter theta를 새로운 h(x)에 넣어주면 된다.

결국 hypothesis는 1이 될 확률을 의미하는 것이다.
Decision boundary.

앞에서 봤던 위와 같은 형태의 logistic에서 언제 1으로 판단하는지, 언제 0으로 판단하는지에 대한 결정값을 설정하는 단계이다.
-suppose predict “y=1” if h(x) >= 0.5 and predict “y=0” if h(x) < 0.5

결국 h(x)가 0.5보다 크려면 g function이 0보다 크면 되는 바이다. 그에 따른 theta.T*x<0이 성립되어야 한다는 것이 정해진다.
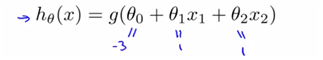
hypothesis값이 이렇게 정해졌을 때, 우리는 언제 0으로 분류하고 언제 1로 분류하는 가를 알아야 할 필요가 있다. theta값을 임의의 값으로 정해줬을 때, 앞에서의 logit함수의 특징에 따라,

g값이 0보다 클 경우에 y=1로 predict하다는 것을 알 수있다. fixed theta값에 대하여 모델 을 fitting해준 후 식을 그래프에 그려본다면 위와 같은 형태의 boundary로 나눌 수 있을 것이다. (y=0으로 predict하는 경우도 마찬가지이다. ) 그리고 우리는 그 선을 decision boundary라고 부른다. (여기서는 시각화를 잘 하기 위해 그래프로 그렸지만 그런식으로 시각화하지 않더라도, parameter of hypothesis를 나타낼 수 있기만 하면 된다. )
2. Logistic Regression
이제 문제는 어떻게 theta를 정확하게 fit된 theta를 구하느냐의 방법이다. (앞에서는 theta를 임의로 두고, hypothesis를 완성하여, 어떻게 1과 0으로 분류하느냐에 초점을 맞췄기 때문이다.)
-Cost function
-선형회귀와 같은 J(theta)를 사용했을 때의 문제점.
logistic에서의 cost function도 결국 linear의 형태와 비슷하게 표현해 볼 수가 있는데,
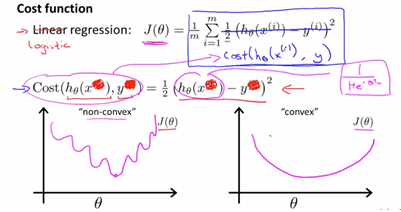
J(theta)식에서 sigma뒷부분을 cost(h(x),y)로 둔 형태로 정의가 가능하고 우리는 이 형태를 logistic의 cost function이라 할 것이다. 이 형태는 non-convex의 형태고(non-linear형태의 logit function의 형태를 h(x)가 가지고 있기 때문이다 ), 이는 global optimum이 아니라 local optimum을 찾아가게 될 것이다. 따라서 우리는 다르게 정의한다.
-penalty를 준 형태로 사용하는 logistic의 J(theta) (convex형태를 위해)
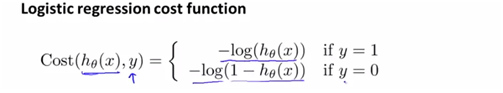
위를 plot해보면 아래와 같다. 애초에 h(x)는 logit을 적용한 형태이므로 0~1사이의 값에 있다. 이 x축값에 따른 y축값을 그리면 다음과 같다.

-y=1인 경우에, h(x)=1이면 cost값이 0이므로 매우 좋은 상태임.
-하지만 h(x)->0이면 cost0->inf.이므로 very large cost 형태가 되고, 좋지 않은 상태.
직관적으로 생각했을 때, h(x)는 y=1일 확률인데 실제로 y=1일 때 h(x)=0이라는 것은 실제로 말이 안되므로 비용이 무한대로 증가하는 것과 같다.
(이런 경우, 즉 h(x)->0의 경우는 y=0의 경우로 생각을 해야 하겠다. )
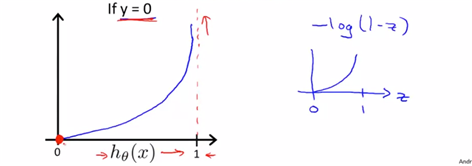
-y=0의 경우는 h(x)=0일 때 cost=0이므로 매우 안정적인 값이 될 수 있다고 본다.
따라서 아래의 새로운 logistic regression cost function을 이용하면 J(theta)를 convex-function의 형태로 만들 수가 있다.
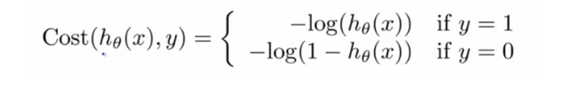
_-simplified cost function and gradient descent _
앞에서 봤던 logistic cost func.를 단순화하는 방법과 gradient descent를 적용하여 optimized theta값을 찾는 방법에 대해 알아보고자 한다.
(앞에서까지 설명했었던 식을 아래와 같다)

y=0,y=1의 경우에 대해 하나의 식으로 compress할 수 있는 하나의 식을 제시.
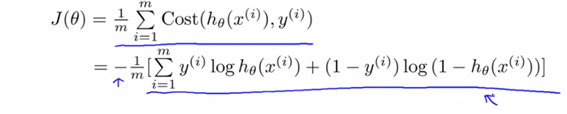
(if y=1의 경우, if y=0의 경우를 각각 식에 대입해보면 원래 구했던 식과 동일하게 된다. 이 cost function은 MLE로 증명이 가능하다. )
-이제 결국 fit parameters theta값을 찾기 위해 minJ(theta)를 하는 theta값을 찾을 것이며, 이 theta값을 h(x)에 대입하는 것이 최종 output이다. 다시말하지만 h(x)는 prob of 1이다. (=1이 될 확률)
-and min J(theta)의 방법을 gradient descent의 방법이다.

repeat항에 있는 sum함수는 J(theta)에 대한 theta의 partial derivitive를 의미한다. (점진적으로 update theta) 또한 이 알고리즘을 결국 identical to linear regression! 결국 바뀐 것을 h(x)이 logit함수를 적용한 형태라는 것 밖에 없다.
-advanced optimization
logistic gradient descent의 성능을 높일 수 있는 방안, large number of features가 있을 때에 대한 대처방안에 대해 설명한다.

gradient descent뿐 아니라 optimized algorithm에는 여러 가지가 있다. 이 알고리즘들의 장점은 learning rate를 고를 필요가 없고 대부분 gradient descent보다 성능이 좋다는 점이다. 그러나 더 복잡하고 라이브러리마다 구현이 다를 수 있으며 디버깅이 핌들 수 있다.
3. Multiclass classification(One vs All) using logistic
- binary에서는 단순히 sigmoid에서 idea를 얻어, 직선으로 class를 구분하는 모습을 보였었다. 하지만 multi class의 경우는 어떻게 나눠야 할까? -> One-vs-all 방법을 사용
- One-vs-all(One-vs-rest) 각각의 다른, 여러개의 이진분류기를 만드는 방법을 의미한다. 즉 하나를 정하고 그 나머지와 분류하는 형태의 이진분류를 시행하는 것을 의미한다. 이것은 class의 개수만큼 진행이 가능하다.
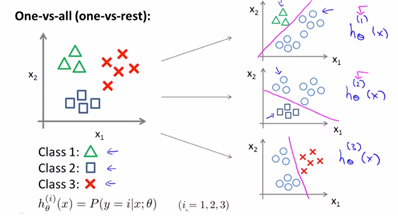
위와 같은 경우는 class가 3개이기 때문에 I=1,2,3으로 나눌 수 있고, I에 따라 이진분류한 hypothesis에 따라 h(x)를 ith에 따라 나눌 수가 있다. 첫 번째 분류기는 세모를 구분하는 이진분류기, 두 번째는 사각형을 분류하는 이진분류기..이다. 따라서 새로운 무언가가 input으로 들어왔을 때, 각 이진 분류기 중 h(x)를 최대로 해주는 I를 선택하면 된다. (highest prob. to predict that value임을 의미하기 때문. h(x)의 정의에 의하면 그렇다=1이 될 확률을 구하는 것과 같다고 정의되므로)

5. The problem of Overfitting
(1) regularizatinon regression working poorly하게 만드는 것이 overfitting이다. 즉 learning model의 성능ㅇ을 향상시키려면 overfitting문제를 해결해야 한다.

즉 trainset으로 전체 데이터를 일반화하기 어려울 정도로 많이 학습시켜 오히려 testset에 대해서는 성능평가지표가 낮게 측정되는 것을 의미한다.
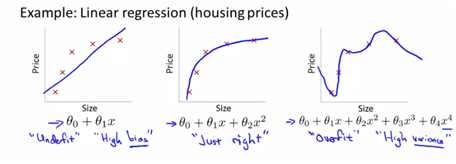
ex) predict house price
- 1차식으로 fitting하는 경우 : trainset에 잘 맞지 않음 -> “underfit”, “high bias”
- 2차식으로 fitting하는 경우 : trainset에 적당히 잘 맞는다
- 4차식으로 fitting하는 경우 : trainset에는 매우 잘 맞음 -> “overfitting”, “high var.”
-이와 같은 overfitting의 형태는 linear뿐 아니라 logistic에서도 나타날 수 있다
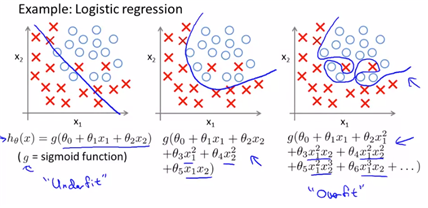
-addresing overfitting
-
이전까지 봤었던 저차원의 feature에 대한 데이터는 plotting하는 형태로 나타내어 잘 맞는지만을 확인하면 됐었다 하지만 feature의 수가 많아지면서 눈으로 확인하기가 어려워진다. 즉 주로 Overfitting은 training set이 부족하고 feature이 많을 때 발생한다.
- 이를 해결하는 방법으로는,
- Reduce number of features
- manually select which features to keep
- Model selection algorithm(later in course) but 이 방법은 useful information loss의 단점이 있을 수 있다.
- Regularization
- keep all the features but reduce magnitude/values of parameters
- works well when we have lot of features, each of which contributes a bit to predicting y. (각 feature가 prediction에 얼마나 기여하는지를 변경)
(2) cost function how regularization work에 대한 직관과 the cost function that we’ll use then we were using regularization에 대해 설명할 예정이다. regularization은 모든 모수를 유지하되, 기여하는 바를 다르게 하여 hypthesis를 simplt하게 만듦으로써 overfitting을 방지하는 방법이다.
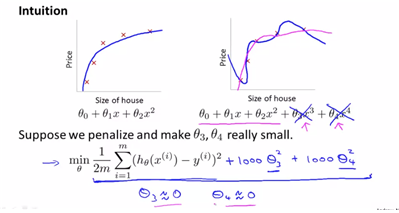
regularization은 원하는 parameter가 hypothesis에 기여하는 바를 조절하는 것이다. theta3, theta4를 cost function에 추가하되 이를 min하게 하려면 theta3, theta4가 0에 가까운 값이 되는 수 밖에 없어야 한다.
-paramters가 작은 값을 가질수록 간단한 hypothesis가 나오고, overfitting하지 않게 된다.
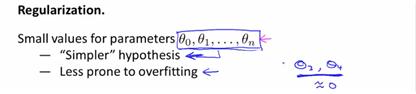
하지만 어떤 parameter가 중요한 feature에 대한 정보를 가지고 있는지를 알 수가 없으므로, 전체 parameter을 shrink하는 과정을 채택한다. 이에 따라 linear reg.의 cost function에 새로운 regularization term을 삽입하여, 모든 parameter값을 작게해준다.
또 주의할 점은 theta0은 regularization을 적용하지 않는다는 점이다.
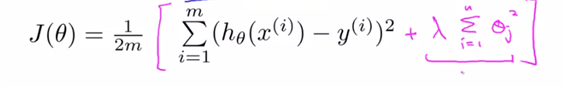
하지만 lamda값이 매우 크다면 theta1~thetan의 값은 모두 0의 값에 수렴하게 되며 underfit하게 된다.
lamda는 regularization paramter이며, tadeoff를 할 수 있다. J(theta)에서의 첫 번째 teram을 데이터와 hypothesis가 잘 맞게 해줘야 하며, 두 번째 term에서 각 theta값들을 적절한 크기로 조절해 줘야 하는 역할을 가진다.
(3) Regularization-regularized linear regression min J(theta)를 하는 방법에는 gradient descent방법과 normal equation방법이 있다고 배웠다. 또 regularization cost function에 gradient descent를 적용한다.(주의할점은 regularization term은 j가 1부터 시작하는 값이므로, theta0인 부분만 따로 빼서 작성하는 것이 옳다)
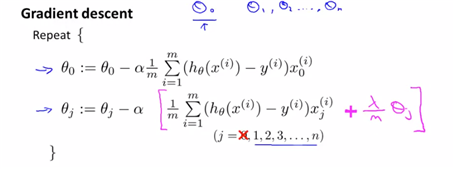
그리고 결국 두 번째 term은 아래의 것을 계산한 것과 동일한 term이다.


-이제 noraml equation에 어떻게 적용할지를 설명한다.
원래 noraml equation은 아래와 같다.
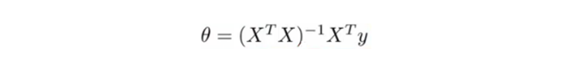
원래 noraml equation의 theta값은 J(theta)를 theta로부터 (partial derivitive=0)를 하여 얻은 theta값이다. 이에 대해 다시 theta값을 정리하면 아래와 같다.
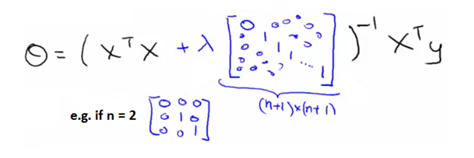
(4) Regularized Logistic Regression
very highly polynomial 식을 사용하고 이를 logit function에 넣어 hypothesis를 완성하여 decision boundary를 지정하면 아래와 같다.
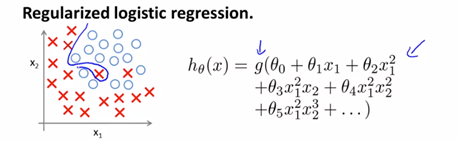
또, 이 logistic에 대해 cost function은 아래와 같다.
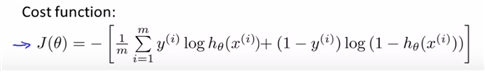
하지만 a lot of features에 대해 overfitting의 위험이 있으므로, regularization cost function으로 modify하여 theta값을 찾아줄 필요가 있다고 판단한다.
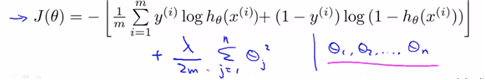
위와 같은 regularizazed J(theta)를 작성한다면 gradient descent 나 normal equation방법으로 theta를 구할 수가 있다. linear regession에서의 gradient desecent regularization과 동일하다. theta0, 나머지로 분리하여 regularization term을 부여하는 것. 하지만 다른 점은 h(x)식이 logit을 적용한 함수라는 점이다.

-non-linear decision boundaries
현재는 binary형태를 보고자하므로 feature가 x1, x2의 2가지 밖에 없다. 이에 대해, h(x)를 보고자 한다. (보다시피 polynomial)의 형태.
linear일 때와 동일하게 임의로 theta값을 정해주고 predict하도록 x값을 정해준다면 circle형태의 decision boundary가 생성된다.

즉 theta값이 정해지면 trainnigset을 이용하여 bondary를 정해줄 수 있다고 본다. and more higher other polynomial에 대해서도 결국 마찬가지이다. (oval형태일 뿐)
reference
Machine learning my Andrew Ng, Coursera