ML02.Gradient Descent
1. Multivariate linear regression
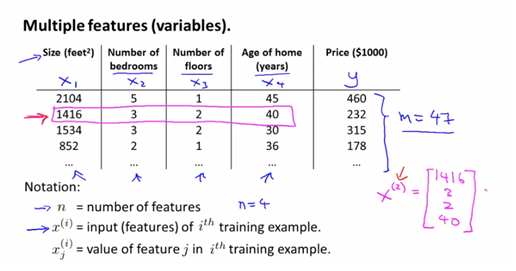
여기서 I는 각 데이터 set들의 index를 의미한다. j는 I번째 set의 jth값을 나타낸다고 본다.
hypothesis :
(predict the price of the house, and features are many)
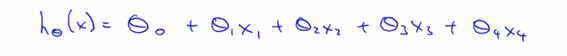
and want to simplify this notation.
x와 theta 벡터를 각각 정의한다면 두 벡터의 dot으로 간단히 정의가 가능하다.
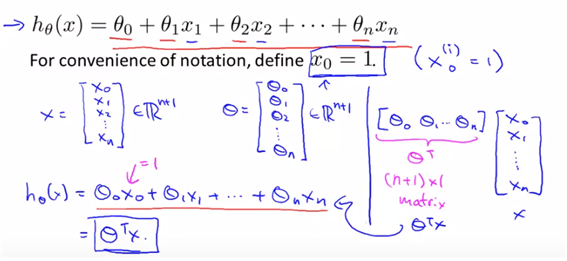
2. gradient descent for multiple variables
how to fit the parameters of the variables.
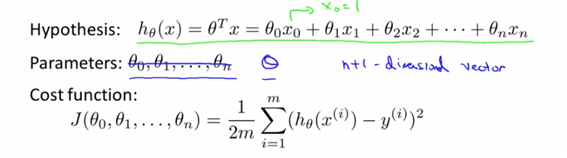
위는 앞에서의 multivar.의 내용을 정리한 것이다. 이에 대해 theta는 (n+1)개로 나누어져 있지만 단지 big theta의 형태로 치환하여 생각하고 하나의 theta에 대한 식으로 생각할 수도 있다.
그리고 우리는 현재 fit된 optima parameter을 찾는 과정이므로 마찬가지로 gradient descent를 사용하여 계산하면 아래와 같다. (gradient descent를 사용하는 이유는 min cost function을 찾기 위해서 이므로)
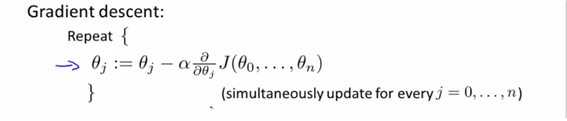
week1에서는 j=0,1뿐이었기 떄문에 각각에 대해 각각 계산해주었었다.
결국 n>=1의 경우에는 n=1에 대해 계산해주는 경우와 동일하다. (다만 partial derivitive해주는 변수만 달라질 뿐이다)

(결국 n=0의 경우도 동일하지만 define x0=1이므로, 따로 정의되는 바이다. ) ->more than one features의 경우에도 same simulationsly update가 가능하다.
3. Gradient descent in practica1-feature scaling
skills for good gradient descent working.
idea : feature scaling-make sure features are on a similar scale.
ex) x1=size(0-2000feet)
x2=number of bedroons(1-5)
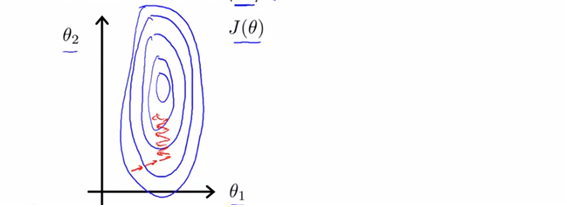
scale상에 있어서 이렇게나 큰 차이가 있다면, gradient descent를 실행하는데도 많은 시간이 소요될 것이다. (더 tall skinny contour이 된다면 gradient descent는 더 많은 시간을 필요로 할 예정이다. ) ->따라서 scale the feature이 필요하다.

scale할 경우에 더 효율적으로 direct gradient descent를 진행할 수 있게 된다. (scale-> 0<x1<1, 0<x2<1)
feature scaling -> get every feature into approcimately a –1<xi<1 range. (꼭 –1~1값이 아니어도 비슷한 형태의 scale이면 인정을 한다. 너무 작은 scale이거나 너무 큰 scale의 경우에는 인정하지 않는다고 본다)
one of the scaling method is mean normalization.(정규화시키는 것도 scaling의 하나의 방법이 될 수 있다.-generally, 표준화식과 동일하다. )

4. gradient descent in practice2-learning rate
another pracical trick to gradient descent work well.
- gradient descent “debugging” : how to make sure gradient descent if working correctly.
- how to choose learning rate a.
gradient descent의 역할은 결국 J를 min하게 하는 theta값을 구하는 과정이다.
반복의 수가 많아짐에 따라 J가 점차 작은 값으로 수렴되는 것을 볼 수가 있다.
따라서 어떤 알고리즘이 몇 번의 iteration을 사용해야 하는지를 알 수가 없다.
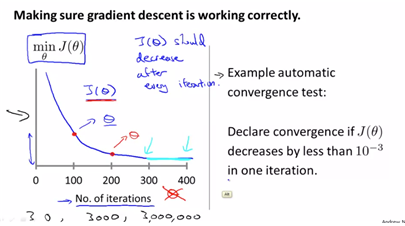
making sure gradient descent is working correctly하기 위해서는 a값에 대한 조절필요 -a가 big이면 overshotting이 일어난다 > use smaller a ->j(theta)값이 커지는 형태가 나타나거나 계속 올라갔다 내려갔다가 반복되는 형태로 나타난다(overshotting되는 형태)
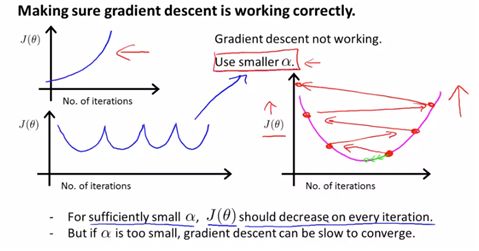
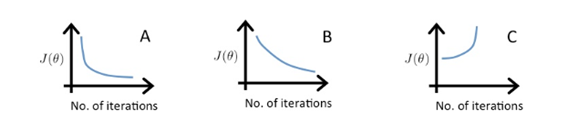
이는 각각 a=0.1, a=0.01, a=1일 때의 그래프를 나타낸 것이다. A와 B가 헷갈리기 쉬운데, A가 더 급격한 변화가 일어나므로 a가 더 큰 값이라고 판단해야 한다.
-if a is too small, slow convergence, -if a is too large, J(theta) may not decrease on every iteration; may not converge.
5. features and polynomial regression
choice appropriate features and usage of nonlinear functions.
polynomial은 결국 다항함수로 나타내지는 회귀식을 의미하지만 결국은 이것도 linear의 일부의 형태이다. non linear이 되는 것은 y에 달린 것이지, x에 따른 것이 아니라는 것이다.
집값을 예측하기 위해 frontage와 depth라는 변수가 존재한다. 이 두 변수를 사용하여 area=frontage*depth변수를 생성하여 집값을 예측한다고 하자. 즉 기존의 변수들을 사용ㅎ여 새로운 변수를 만들어 간단한 식을 작성할 수 있는지의 여부도 중요하다.
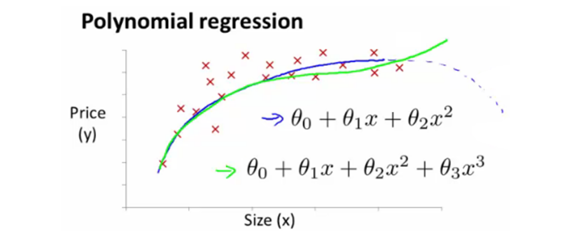
집값을 예측하는 함수의 경우에 quadratic을 세우면 어느 지점부터는 예측된 값이 감소되어야 한다. (하지만 그렇지 않으므로) cubic 다항식을 이용하여 식을 세운다. (size를 이용한 3차식)
여기서 quadratic은 다항식으로 계산하는것을 말한다. (data에 더 fit하는 reg.를 찾기 위한다.)
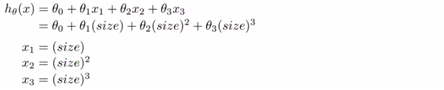
(각각의 size의 제곱, 세제곱을 다른 x1, x2…의 값으로 치환이 가능하다고 말해주는 것이다)
하지만 x1, x2, x3의 range가 큰 차이가 있으므로 scaling문제에 있어서 문제가 될 수도 있겠다. (apply feature scaling for gradient descent)
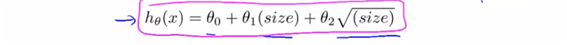
혹은 이런 형태로 식을 지정할 수도 있다.
Computing parameters analytically
7. noraml equation
can give much better way to solve for optimal value of the parameters theta. 우리는 이제까지 gradient descent를 이용하여 J(theta)를 최소화해주는 theta를 찾았다. 이에 대해,
- normal equation : Method to solve for theta analytically이다.
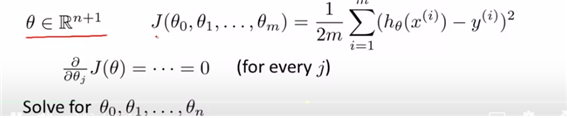
when to use gradient descent or normal equation

(normal equation은 결국 design matrix를 이용하여 theta값을 구해야 하는 경우이므로 위와 같은 행렬값을 계산해야 한다는 이야기 )
8. noraml equation noninvertibility

non-invertible 이라는 것은 결국 AB=BA=I를 만족시키는 B가 존재하지 않는 행렬 A를 의미한다. (이것을 Octave에 입력하려면 pinv, inv를 사용한다. (pinv를 대부분 사용한다))
우리가 계산해야 할 행렬이 non-invertible이라면 두가지 경우일텐데, (1) Redundant features(linearly dependent) (e.g x1 = (3.28) * x2)-linear관계의 x1, x2 (2) too many features (e.g m <= n) (10개의 dataset을 가지고 있는데 100개의 feature을 가지고있는 경우) 이런 경우에는, 몇 개의 feature을 제거하거나 regulazation을 사용한다.
reference
Machine learning my Andrew Ng, Coursera