ML01. Linear regression
1. machine Learning
-Grew out of work in AI -New capacity for computers ex) database minig, 손글씨 인식, 드론 작동, NLP, 초개인화 알고리즘 등
2. what is machine learing?
-프로그램이 일정수준의 작업 성능(P)을 가지고 작업(P)을 수행한다고 했을 때, 경험(E)이 증가함에 따라 작업(T)를 수행하는 성능이 향상될 수 있습니다. 프로그램이 경험을 학습했다고 말할 수 있다. machine learning algorithms: -Supervised learning : 작업을 수행할 수 있는 방법을 컴퓨터에 학습 -Unsipervised learning : 컴퓨터가 스스로 학습하도록 하는 것 -others : 강화학습, 추천시스템 • E: Wathing you label emails as spam or not spam. • T: Classifying emails as spam or not spam. • P: The number(or fraction) of emails correctly classified as spam/not spam.
3. Supervised learning
Given the “right answer” for each example in the data.
Regression의 경우 : Predict continous valued output.
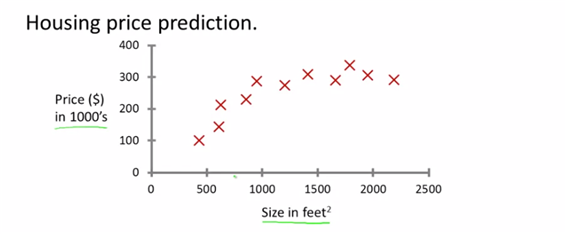
집사이즈에 맞춰 값을 예측하는 방법 : 직선으로 맞출지 혹은 곡선으로 맞출지 고민할 수 있다. 지도학습이란 모델에 답을 알려주는 것이다. 실제 집의 가격을 알려줌으로써 알고리즘을 작성한다. 그리고 더 많은 ‘정답’을 알고자 하는 것
Classificatino의 경우 : Discrete calued output(0 or 1)
종양사이즈에 따라 악성종양인지의 여부를 분류하는 경우
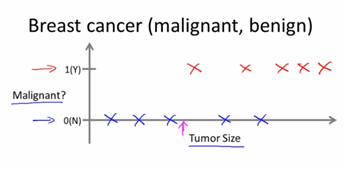
일수도 있고 혹은 더 많은 특징을 공유할 수도 있다.
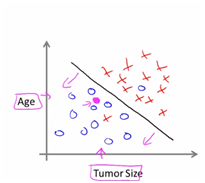
하지만 무한한 개수의 특성을 다루게 될 때는? 나중엔 SVM모델을 사용하여 모든 특성을 다룰수 있도록 하는 수학적인 특성을 사용할 것이다.
4. Unsupervised Learning
대표적인 것은 clustering과 cocktail party problem(2명이 동시에 말하고 이것을 구분할 수 있는가에 대한문제) 지도학습에서는 명시적으로 ‘정답’이 주어진다. 즉 양성인지 음성인지를 판단해야 한다..등 하지만 비지도 학습에서는 어떤 레이블도 갖고 있지 않거나 모두 같은 레이블을 갖고 있거나 또는 아예 레이블이 없을 수도 있다. 즉 우리는 단지 ‘여기 데이터가 있는데 이 데이터는 어떤 구조를 가지고 있습니까?’를 묻는것과 동일하다고 본다 ex)구글 뉴스 : 기사들을 비슷한 topic별로 묶어서 나타내준다. 유전학적 자료의 경우 : 서로 다른 사람들에게서 특정 유전자가 얼마나 발현 되는지를 보고자 하는 것. 어떤 데이터가 무엇을 뜻하는지를 알려주는 것이 아니라 여러개의 데이터 중에서 이런걸 제시하면 무엇을 의미하고 전체적으로 분해했을 때 어떻게 나눌 수 있는지를 알려주기를 원하는 것이기 때문에 비지도 학습임. 알고리즘에게 정답을 학습시키는 경우가 아니기 때문에 비지도 학습.
5. model representation
size를 주고 price를 예측하고자 할 때는, supervised learning이 가능 : given “right answer”
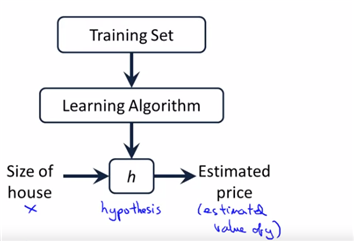
여기서의 h는 hypothesis즉 가설을 의미하며, x가 x’, y’로 mapping되는 과정을 의미한다고 본다. (식으로 표현되는 과정이라고 이해하면 된다)
6. cost function
we will show how to fit the best straight line.

결국 위의 선형식에서의 계수가 parameter즉 구하고자 하는 모수 이므로, 이를 구하는 (=best fit)되는 직선이 어떻게 나오게 되는지를 구한다.
data에서는 우리는 training set은 반드시 가진다. 이에 대해 straight line을 그리면 theta0, theta1값을 모두 구할 수가 있다.
idea : choose theta0, theta1 so that h(x) is close to y for our training examples(x,y)

(h(x)는 실제 data를 fit하여 구하여 estimate한 값이고, y(i)는 실제로 ith를 ‘관찰’했을 때의 값이다. 이에 대해 오차를 최소화해야 되므로, minsqure을 했으며, 계산식을 최소화하기 위해 1/2m을 해주었다.)
결국 위의 식에서 h(x)식이 theta에 대해 표현이 되는 식이기 때문에, 결국은 theta를 모수로 가지고 있는 식이 완성이 된다. (이를 좀더 간단히 쓰자면 아래와 같다)
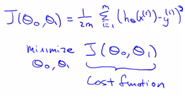
즉 cost function은 손실함수를 의미하며, 결국은 ‘오차’에 대한 이야기를 하게 된다. 즉 smaller values of the cost function correspond to a better fit이므로, 작으면 작을수록 좋다. 즉 (estimator-real value)의 mean squre값이 작으면 작을수록 좋다(=오차가 작으면 좋다=cost function이 작아진다)라고 정의가 가능하다. 이를 J function 이라고 notation을 붙인 것 뿐이다. (왜? 결국은 모수 theta0,theta1을 최소화하게 하는 costfuction이므로 해당 모수가 theta) ==squeared errer function
-costfunction intuition1 앞에서 cost function 즉 squared error function의 정의에 대해 봤다면 간단한 예시와 우리가 이걸 왜 배우는지에 대해 살펴볼 예정이다. 앞에서 배웠던 식은 다음과 같다.

즉 min(cost function)이 주된 목표이자 optimization object라고 볼 수가 있다. 그리고 simplified된 형태로서 그냥 theta0=0으로 두고 정의를 하기도 한다.(직관적으로 식을 더 이해하기가 쉽기 때문에, 또 theta0보다는 결국 theta1이 parameter간의 관계를 보여주는 척도이기 때문에 그렇게 나타내기도 한다)
ex1) theta1=1인 경우
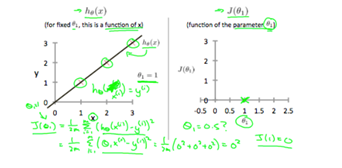
즉 J(theta1)=0 (결국 real value인 세 점에 대한 error의 squared값이므로 0이 되는건 당연)
ex2) theta0=0, theta1=0.5인 경우
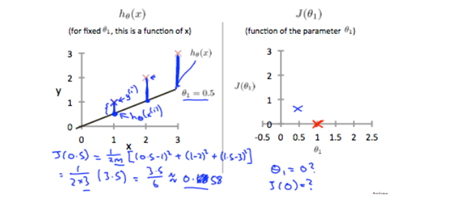
마찬가지로 J값에 값을 대입하여 계산하면 0.58값이 나온다.
ex3) theta0=0, theta1=0의 경우 horizental한 곡선과 real-value간의 err의 제곱을 구하게 되고 (1^2+2^2+3^2)/2*3이므로 14/6=2.58이다.
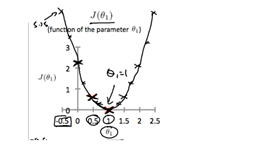
즉 J(theta1)은
즉 real-value=estimated-value인 theta1=1인 경우만 제외하고는 나머지는 err값이 존재하므로 J값은 그 squared값이므로 큰 차이가 나게 되는 것은 어찌보면 당연한 결과.
-cost function intuition2 앞에서 제시했던 형태는 theta1에 대해서만 고려했던 값이므로 bowl-shaped로 J를 그릴수 있었다. 하지만 이제는 theta0, theta1을 모두 고려하는 형태를 보려 하므로 투시도로 그릴 수밖에 없다. 즉 축이 하나더 생기는 형태로 그려야 한다.
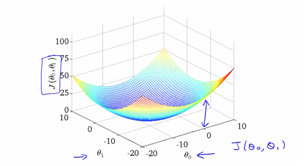
하지만 theta값이 2개가 되어 contour값이 되었을 뿐이고, 이론은 위와 같을 것이다. 각 estimated된 직선에 대해 real-value와 의 squared error값을 각각 찍어 그린 값이다. 이를 등고선 plot으로 생각하여 구하면 아래와 같다.(등고선 plot에서는 같은 J값을 가지는 점들끼리 같은 oval로 표시가 되어 있다.). 이 궤도를 해석하는 방법 : 앞에서 2차원으로 표현할 적에는 theta1과 J를 plot에 나타내었다. 이 등고선그래프에서는 (theta0, theta1)만을 2차원적으로 나타내며, 같은 궤도에 있는 값들은 동일한 J(theta)값을 가진다. 또 궤도가 가장 좁은 타원의 중심의 좌표들이 가장 작은 J(theta)값을 가진다고 해석하면 된다.
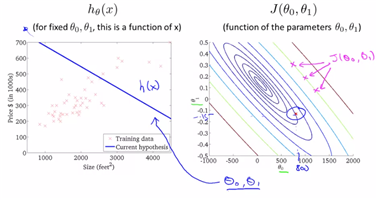
우리는 단지 min값의 theta집합을 구하고자 하는 것이다. 즉 theta값들은 2개가 아니고 여러개일 수도 있다.. 따라서 우리는 theta0, theta1을 automatical하게 찾을 수 있는 방법을 알아야 한다.
8. Parameter Learning
-gradient descent min{ J(theta0, theta1) }에서의 theta0,theta1을 구하기 위한 방법이다. 하지만 머신러닝에서 범용적으로 사용이 가능하다.(linear regression에서 뿐만이 아니라) 따라서 이후에는 regression뿐만이 아니라 다른 함수를 최소화하는 모수를 구해볼 것이다.
2개의 모수 뿐만이 아니라 n개의 theta에 대해서도 계산이 가능하다는 점.

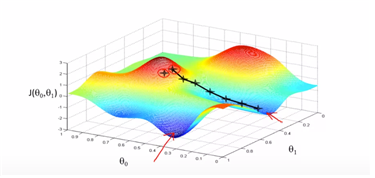
이 상태에서 첫 번째 점에서 시작하면 점진적으로 이동해 가면서(높이를 비교해가면서 ) first local optimum지점에 도착할 것이고, 만약 조금더 옆으로 이동한 두 번째 점에서 시작을 하게 된다면 second local optimum지점에 도착을 하게 될 예정이다. 즉 initiation점에 따라 다르게 도착하기도한다.

-알고리즘 식은 위와 같은데, :=은 assignment식(할당식)을 의미한다. 단지 =식은 (truth식을 의미한다. Octave에서는) -a는 learning rate를 의미한다. 즉 ‘how large step that we step down’을 의미한다. 즉 얼마나 점진적으로 이동하는지를 나타낸다 -마지막은 편미분식으로 각 theta식에 대해 기울기를 구하는 식이다. (두 모수에 대해 모두 최솟값인 theta를 구해야 하므로 각각에 대한 편미분 식을 사용하게 된다) –>sumultaneausly update theta0 and theta1 (이때 theta0, theta1값은 동시에 update되어야 한다.)
-gradient descent intuition

gradeint descent식은 위와 같고 이를 분해한다. 여기서는 learing rate와 derivative term이 각각 무엇을 의미하고 왜 있는지에 대해 설명할 예정이다.
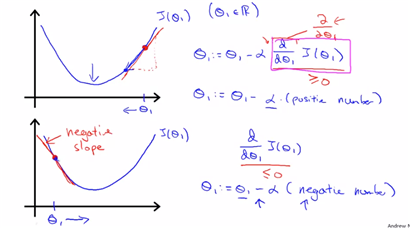
- if a is too small, gradient descent can be slow
- if a is too large gradient descent can overshoot the min. It may fail to converge, or even diverge.
-하지만 이 gradient descent 의 문제점은 ‘local’ optimum이 존재하는 경우이다. global optimum을 구하지 못하고 local점에서 멈추게 된다.
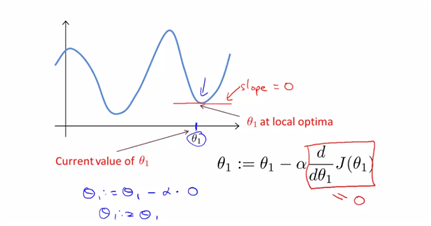
gradient descent can converge to a local minimum, even with the learning rate a fixed. as we approach a local minimum, gradient descent will automatically take smaller steps. So no need to decrease a over time.

-gradient descent for linear regression put together gradient descent and cost function and fitting a straight line for out data.
apply gradient descent to J
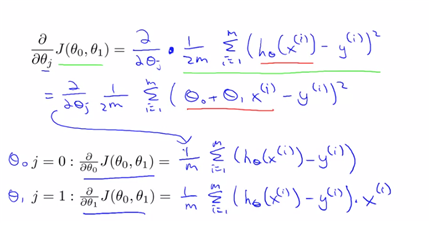
(이는 사실 단순히 cost fuction에 gradient descent 값을 넣고 정리한 것에 불과하다) 정리하면 아래와 같다.

-> and update theta0 and theta1 simultaneously
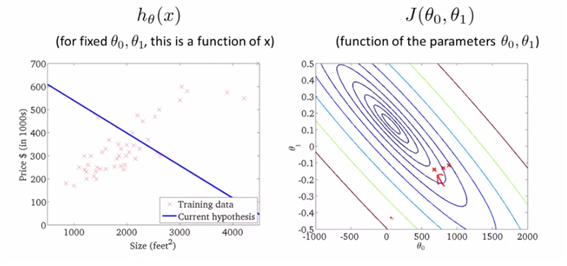
즉 cost function에 gradient descent를 적용하여 fitted 값을 구하고자 하면 위와 같을 수 있다. gradient descent algorithm을 이용하여 theta0, theta1의 값을 정할 것이고 그에 다른 J값도 정할 수 있으니 그것을 이용하여 h(x)를 구해주면 cost를 최소화하는 h(x)를 그려볼 수 있을 것이다.
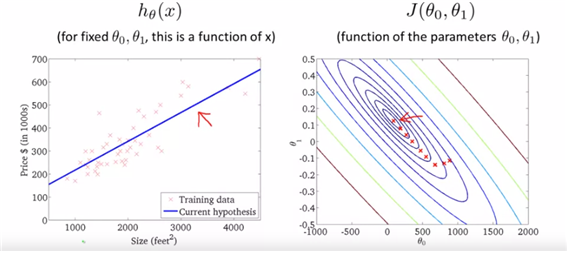
->can determine good fit and can predict house price
Batch Gradient descnent는 모든 training examples를 사용하는 경우를 의미한다. (m개의 example을 사용하는 것을 의미한다) 즉 small subset만을 사용하는 경우도 존재할 것이라는 의미. Gradient descent can converge even if α is kept fixed. (But α cannot be too large, or else it may fail to converge.) For the specific choice of cost function J(theta_0, theta_1)J(θ0,θ1) used in linear regression, there are no local optima (other than the global optimum).
reference
Machine learning my Andrew Ng, Coursera